Stan and His Students

When Stan Fischer was a professor at MIT, he was one of the all-time great advisers to those of us in the process of becoming macroeconomists.  At a recent conference, Stan took a picture with some of his former students.  Here is the snapshot.  How many can you recognize?

To QE or not to QE?

The FOMC meets today and tomorrow. Here's what the committee members will be discussing. Since May, expected inflation has fallen and real bond yields have risen, as you can see in the first chart.

The chart shows the breakeven rate (10-year nominal Treasury yield minus TIPS yield) and the 10-year TIPS yield. The breakeven rate tends to be biased upward as a measure of anticipated inflation (TIPS insure inflation risk, and a TIPS-holder does not have to pay the Treasury if the CPI inflation rate falls below zero), but typically moves in the same direction as anticipated inflation. As well, if we compare the path for the PCE deflator to a 2% growth path from January 2007, we get the next chart.

Since late 2012, the PCE deflator has been south of the 2% growth trend, and the last observation (May 2013) is about 1% on the low side. If you care about year-over-year inflation rates, you'll come to the same conclusion - the inflation rate is too low, relative to what the Fed wants.

Given that the goal of the latest QE (quantitative easing) exercise, which has been proceeding at a pace of $85 billion in asset purchases ($45 billion in long Treasuries, $40 billion in mortgage-backed securities) per month since fall 2012, was to reduce bond yields and presumably to increase current and anticipated inflation, things are not moving in the right direction.

On the other side of the dual mandate, the unemployment rate is still above where the Fed wants it to be.

An important part of the unemployment story is what is going on with the long-term unemployed, so we can look as well at the long-term unemployment rate (those unemployed 27 weeks or more, as a percentage of the labor force). That's in the next chart.

This is interesting, as about 2/3 of the reduction in the unemployment rate since it peaked has come from decreases in the long-term unemployment rate. You can see that the long-term unemployment rate is still very high relative to where it was before the last recession started (about 2.8% vs. something less than 1%). If the unemployment rate fell in the next months at the average rate of decrease from its peak until now, then it would cross the Fed's 6.5% threshold in about March 2015. This is important, as the FOMC has told us that it will not consider increasing the "fed funds rate target" (actually the interest rate on reserves) until the unemployment rate crosses the 6.5% threshold (and as long as the inflation rate is not too high). Further, Bernanke has told us, essentially in a side conversation, that the policy rate is not likely to increase immediately after the threshold is crossed.

Two points here:

1. If the FOMC wants to be consistent with its previous policy statements, and what Bernanke has said in public, it should plan to purchase assets at a higher rate. The news has been on the down side on inflation, anticipated inflation, and long bond yields, with nothing dramatic happening one way or the other in the labor market. So, in order to keep its promises, there should be more QE, and Bernanke should not be talking about "tapering."
2. It seems almost certain that Bernanke will not be in his current job in six months, so why do we care what he says? If we knew the next Chair would be Janet Yellen, then we care what Bernanke says now, as it seems Yellen would just follow through on that. If Larry Summers gets appointed, then things change entirely. Summers is on record as thinking that QE probably doesn't matter much, and that we might have to revise our views about what the capacity of the U.S. economy is. Maybe QE, thresholds, etc. all go out the window.

In an ideal world, what should the Fed be doing? In the past I've argued that QE shouldn't matter, for quantities and prices. But suppose I were working for the Fed full time, and someone asked me to come up with a rationale for QE. What would I do? The answer is this paper, which is the best I can do at the moment, to come up with a model where QE actually makes a difference. You can read the paper to your heart's content, but here's the idea. To take QE seriously we have to be specific about fiscal policy and its relationship to monetary policy, what private financial intermediaries and the central bank can and cannot do, and the roles of assets in exchange and as collateral. The paper does all that, I think. Start with a world where the fiscal authority is doing something stupid. It issues nominal government debt - in short and long maturities - and sets taxes in such a way that the real value of the consolidated government debt is constant forever, at a value V. The central bank can issue reserves, which are perfect substitutes for short-maturity government debt, and currency. The private sector needs currency for some kinds of transactions, and there are other transactions where people trade intermediary liabilities that are backed by short and long-maturity government debt and reserves. Banks serve to allocate liquidity (currency, reserves, government debt) efficiently to the appropriate transactions. The central bank can execute asset swaps - its job is to manage the composition of the outstanding consolidated government debt, consisting of currency, reserves, short maturity bonds, and long maturity bonds.

But we can't trust banks, which need to (implicitly) collateralize their deposit liabilities. The collateral consists of the bank's assets - reserves and government debt. But collateral is imperfect, in the sense that the bank can abscond with some fraction of any asset in its portfolio (a Kiyotaki-Moore problem). To get a term premium - an upward sloping nominal yield curve, it must be easier to run away with long-maturity government debt. This is definitely a short cut, as I discuss in the paper, but a useful starting point. Also, for there to be a term premium, there must be a shortage of liquidity, i.e. V must be small enough that we can't get efficient exchange - of assets for goods.

What does QE do? A QE experiment involves a purchase of long-maturity government debt by the central bank, holding constant the short-term nominal interest rate. This essentially mitigates the asset shortage. The central bank is swapping good collateral for collateral that is less good. This reduces the term premium, the nominal long bond yield falls, and the yield curve flattens. So far so good for Ben Bernanke. But because collateral is now less scarce in the aggregate, real bond yields rise - at both the short and long end of the real yield curve. Further, the inflation rate falls. That's certainly not how Ben Bernanke thinks QE works. The usual story is that QE will cause real bond yields to fall and inflation to rise. In the model, QE is a good thing to do, though.

Another interesting feature of the model is that, if the central bank holds the short-term nominal interest rate constant at zero, and V increases, then inflation falls, and real bond yields rise. Looks like what is going on in the first two charts, right? V is a convenient catchall in the model. Including private assets in the model (loans, equity) should not be a big deal. Better private opportunities is like having a larger V, and we could also think of higher demand for domestic government debt coming from abroad as lowering V. Currently in the real world, if we think that private investment opportunities are looking better and with a better outlook on sovereign debt problems reducing the demand for U.S. consolidated government debt, we can translate this into a reduction in the scarcity of collateral in the aggregate, and a smaller V in the model. So far so good.

So what does this tell us? We're in a world where real interest rates on government debt are endogenous. Those interest rates include liquidity premia that reflect the marginal value of different classes of government debt as collateral and in financial transactions. Currently real interest rates are going up, so it should not be surprising, with the short-term nominal interest rate pegged close to zero, that inflation is falling. Conclusion: People will definitely call me stupid for saying so, but as Cartman says, screw you guys. The Fed can make all the confusing promises about the future it wants, and purchase all the assets it wants, but it may not be able to increase the inflation rate to the 2% it wants unless the nominal interest rate on reserves goes up. That's what the model says.

The same people who will most certainly be calling me stupid will also want to call me inconsistent, a bad inflation forecaster, or some such. You can go back and read my posts and find me worrying about the potential for inflation that exists in the state of the Fed's balance sheet. Here's Krugman's take on bad inflation forecasters:

I’ve spent five years and more watching the inflationphobes, who weren’t particularly sensible to begin with, descend into shrill unholy madness.

Holy crap, who would want to be one of those inflationphobe characters? To save myself from banishment to Krugmaniac hell, I'm going to appeal to multiple equilibria. I haven't written this up yet, but I've worked out some stuff on what happens when a naive central banker, who follows a Taylor rule, and believes erroneously that the real interest rate is exogenous, goes to work in my model. You can get two equilibria: zero lower bound, low real interest rate, low inflation, or positive nominal interest rate, high real interest rate, and high inflation. That's essentially been my point. There's nothing inherently inflationary about a large central bank balance sheet. The potential for inflation comes from how the central bank behaves given the state of its balance sheet. The multiple equilibrium story is somewhat related to this paper by Jim Bullard, with some important differences, I think.

Trends in Hardware and Software Costs as an Example of Structural Economics Dynamics

Empirical Trends in Costs for Computer Systems

1.0 Introduction¹

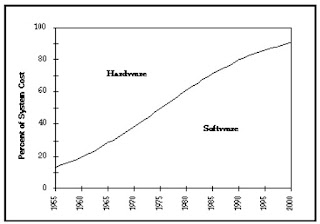
Over time, the proportion of the cost of computer systems consumed by software has tended to rise. Figure 1, originally in Boehm (1973) illustrates. In this post, I offer a theoretical explanation of this empirical observation. One might take this post as an illustration of an empirical use of the Labor Theory of Value.

2.0 The Model

Assume a computer system consists of equal amounts of hardware and software, both measured in some standard units^{1, 2}. Earlier computer systems delivered less units, while current computer systems deliver more. Next, assume that both hardware and software are produced directly from labor³.

2.1 Definitions and Assumptions

Let l_h be the staff-hours needed to produce a unit of hardware. Define ρ_h to be the rate of growth of labor productivity in the hardware industry:

ρ_h = - (1/l_h)(dl_h/dt)

Similarly, let l_s be the staff-hours needed to produce a unit of software, and define ρ_s to be the rate of growth of labor productivity in the software industry:

ρ_s = - (1/l_s)(dl_s/dt)

The last assumption is that the rate of growth of productivity is higher in producing hardware:

0 < ρ_s < ρ_h

One last variable must be defined. Let p be the ratio of labor costs to total system costs for a software system:

p = l_s/(l_h + l_s)

This completes the exposition of the model assumptions and variable definitions.

2.2 The Solution of the Model

Some algebraic manipulations with the above definitions yields the following differential equation:

(1/p) (dp/dt) = Δ(1 - p),

where Δ is the difference in the growth rates of labor productivities in hardware and software productivity:

Δ = ρ_h - ρ_s

This differential equation expresses the rate of growth of software cost, as a proportion of total system cost. The solution to this differential equation is:

p(t) = 1/[1 + c exp(-Δ t)]

where c is a constant determined by an initial value:

c = [1/p(0)] - 1

2.3 Numerical Values

Calibrating the model is the last step in the analysis presented here. Suppose 20% of the cost of a system is software in 1960, and that 80% of the cost of a system is software in 1995. The rate of growth of labor productivity is then 8% more in hardware than in software.

Δ = (1/35)[ln(4) - ln(1/4)] ≈ 7.9 %

The integrating constant for the initial value is:

c = 4/exp(-1960 Δ) ≈ 1.1 x 10⁶⁸

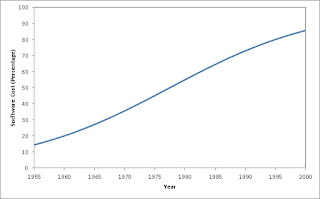
Figure 2 shows the relative proportion of system costs, as generated by the model with these parameters. Notice how closely Figure 2 resembles Figure 1. The model provides an explanation of the empirical observations.

Modeled Trends in Costs for Computer Systems

3.0 Conclusion

This post has presented a model, with its attendant idealizations. And that model shows how the empirical observation that productivity increases faster in hardware than software can account for the empirical observation that the cost of computer systems have become mostly software costs. Hardware costs, as a proportion of total system costs have been declining for decades.

Footnotes

1. This post draws on work I did elsewhere decades ago.
2. Floating Point Operations per Second (FLOPs) is a common measure of output in hardware. I suppose one should also specify the power at which these FLOPs are generated.
3. Source Lines Of Code (SLOC) is a common measure of software size. I have heard the analogy that measuring software in SLOC is like measuring the size of a house by the number of nails used in its construction. I guess one could always use Function Points (FPs) as a measure of software.
4. A natural extension would be to assume both hardware and software are produced solely from inputs of labor, hardware, and software. I am not sure if I ever stepped through such a model in this context.

References

• Barry W. Boehm (May 1973). "Software and Its Impact: A Quantitative Assessment", Datamation.
• Luigi L. Pasinetti (1993). Structural Economic Dynamics: A Theory of the Economic Consequences of Human Learning, Cambridge University Press.

On Au

Click here to read my column in Sunday's NY Times.

The topic is whether you should invest in gold as part of your portfolio.  After you read the column, you might find the following problem of interest.  It is based on roughly plausible assumptions.

Imagine that you start off with a portfolio of 60 percent stocks and 40 percent bonds.  The returns on stocks, bonds, and gold are uncorrelated.  Stocks earn a higher expected return than bonds.  Bonds and gold earn the same lower expected return, but gold returns are three times as volatile as bond returns, as measured by the standard deviation.  You want to minimize risk, measured by the variance of your portfolio return, without changing the expected return on your portfolio. How much gold should you buy?

I will leave this problem as an exercise for the reader.  But I believe you should be able to come up with a precise numerical answer without resorting to a computer.

Update: Albert Zevelev, a grad student at Penn, posts the correct answer here.

Is Technopessimism Bunk?

Yes, says Joel Mokyr.

Who Should Run the Fed?

It seemed like a foregone conclusion that Janet Yellen would be the next Chairman of the Board of Governors (and hopefully would get the powers-that-be to drop the "man"), when Bernanke's term ends on January 31. But apparently some people have other ideas. As today's NYT notes, Larry Summers is being taken seriously as a contender for the job.

If we stick to economic ideas, Yellen and Summers are quite similar. Both are Old Keynesians - they're aware of mainstream macroeconomics, but seem most comfortable with an IS-LM, Phillips-curve view of the world. But if we look at what they have written and said in public, some differences emerge. For example, in this speech by Janet Yellen in April, on "Communication in Monetary Policy," she explains how communication policy has evolved at the Fed, and defends current policy. She thinks that quantitative easing (QE) works as intended:

These [large-scale asset] purchases were intended to, and I believe have, succeeded in significantly lowering longer-term interest rates and raising asset prices to help further the Federal Reserve's economic objectives. This is an easing of monetary policy, also known as accommodation, beyond what is provided by maintaining the federal funds rate close to zero.

Also, the adoption of thresholds for monetary policy actions was a good idea:

I consider these thresholds for possible action a major improvement in forward guidance. They provide much more information than before about the conditions that are likely to prevail when the FOMC decides to raise the federal funds rate. As for the date at which tightening of monetary policy is likely to occur, market participants, armed with this new information about the Committee's "reaction function," can form their own judgment and alter their expectations on timing as new information accrues over time.

These thresholds will, as a consequence, allow private-sector expectations of the federal funds rate to fulfill an important "automatic stabilizer" function for the economy. If the recovery is stronger than expected, the public should anticipate that one or both of the threshold values will be crossed sooner and, hence, that the federal funds rate could be raised earlier. Conversely, if the outlook for the economy unexpectedly worsens, the public should expect a later "liftoff" in rates--an expectation that would reduce longer-term interest rates and thereby provide more-accommodative financial conditions.

Yellen supports the status quo on the FOMC, and there is no reason to think that she would be much different from Bernanke as Fed Chair.

Summers, on the other hand, is quoted in this FT article as being dubious about QE:

QE in my view is less efficacious for the real economy than most people suppose.

Also:

If QE won’t have a large effect on demand, it will not have a large effect on inflation either.

So, on this, Summers and I agree, more or less. If QE matters, it's not for the reasons the Fed thinks, and the consequences may not be what the Fed thinks they are, either. But QE is not inherently harmful, or inflationary. Harm can only come if the Fed has beliefs about QE that are not correct, or if QE somehow causes political trouble for the Fed.

Summers also says (from the same FT article):

If we have slow growth, we are not going to keep thinking that 5.5 per cent unemployment is normal. We are going to decide rightly or wrongly that the potential of the economy is less and therefore we are going to decide that we are closer to that potential and that is going to operate in favour of suggesting that we should normalise interest rates.

That appears to run counter to current Fed forward guidance thresholds. The FOMC consensus appears to be that 5.5% unemployment is normal.

So, Yellen would give us continuity, but Summers might shake things up a bit, perhaps in a good way. But sometimes Summers gets in trouble when he shakes things up. At the World Bank, there was the infamous Summers memo, and he didn't exactly make a lot of friends among female scientists as Harvard President. As economists we might understand better than the average person what Summers was trying to say when he opened his mouth and put his foot in it, but central bankers do well when they have the right filters between brain and mouth.

An important point is that Yellen will not need to go through Senate confirmation to become Chair of the Board of Governors. She was already confirmed to be a Governor, for a 14-year term, in October 2010. The Chair is chosen from among the Governors. In cases where the proposed Chair is not already a Governor, the Senate must go through confirmation proceedings.* Possibly that won't a cakewalk for Summers, and President Obama should be worried about that, if he isn't already. In addition to offending people in developing countries, women scientists, and various faculty members at Harvard, some people have objected to Summers' perceived role in the Shleifer affair, and this may have had something to do with his resignation as President of Harvard. I have no opinion on this, as I don't know anything about it, but obviously some people think they know things, and they have strong opinions. And Summers has to carry that baggage into confirmation proceedings.

But, enough about Yellen and Summers. If you were to ask me (not that anyone is), I would advise following the lead of the Bank of England. Appoint a Canadian! As everyone knows, Canadians have superior leadership abilities, are excellent economists, and understand financial stability really well. But which Canadian? Tiff Macklem, current Senior Deputy Governor of the Bank of Canada, would be great. The fact that he's not a U.S. citizen could put the kabosh on that idea, but maybe he's a secret American - his mother took a trip to Plattsburgh to give birth, or some such.

*See the comment below.

A Tale of Two Political Systems

Here is a fascinating TED talk about the Chinese political culture.  It takes about 20 minutes.

Addendum: And here is a thoughtful commentary on the talk.

Geography and Mobility

A former student, M. Daniele Paserman, who is now a professor at Boston University, sends me the following email, which I thought was interesting enough to share (with permission, of course):

I bumped into your blog post on the Great Gatsby curve, and I was happy to see you raise the point about the arbitrariness of imposing geographic boundaries in measuring intergenerational mobility (why should one lump Connecticut and Mississippi together?)

Claudia Olivetti and I raise a similar point in our recent paper on the evolution of intergenerational mobility in the US between the end of the 19th and the beginning of the 20th Century. We measure a large increase in the intergenerational elasticity between the the cohort of children born in the 1850s and those born in the 1910s, but almost all of it can be explained by income divergence across regions. In fact, within the Northeast and the Midwest, the intergenerational elasticity was flat, or maybe even falling (it was rising in the South, though).

Capital Income Taxation

Alan Viard offers his perspective on this key debate.

New Keynesian Models and Monetary Policy

For people who want a basic explanation of where New Keynesian models came from, why central bankers find them attractive, and a critique, from a policymaker's point of view, this speech from a couple of months ago by Charles Plosser is helpful.

Elsewhere

• Steve Denning, a writer for Forbes, describes Milton Friedman as being the source of "The world's dumbest idea". (I have written on Milton Friedman's confusion. incoherence, and lack of integrity, as well as Michael Jensen's (ir)responibility. See also Unlearning Economics.)
• Mike Konczal on Philip Mirowski's new book.
• Henry Scowcroft on the need for communicating economics to the public.
• Michael Lind on supposedly "Econ 101". Noah Smith complains about the public impression of what economists teach.
• Robert Neild on a 1981 anti-monetarism petition. I am especially amused about him losing his cool in a debate with Milton Friedman.
• Mark van Vugt and Michael Price, two psychologists, I gess, comment on Homo Economics. They link to a website which has David Sloan Wilson as editor in chief.
• Floyd Norris, in the New York Times, explains that Steve Keen foresaw the global financial crisis better than Ben Bernanke did.

Selgin Update

George Selgin had a bad experience with a commenter on this post. I know how he feels. It's too bad if some people accept as gospel that some ideas are good, evil, right-wing, or left-wing, and suspect the motives of people they think are on the other side of the political divide. It's hard to have a sensible discussion about economics in that context.

The Changing Distribution of Income

Click on graphic to enlarge. 



Mark Perry points out: "Yes, the middle class has been disappearing, but they haven’t fallen into the lower class, they’ve risen into the upper class."

Who Are The Nine People Prosecuted By The USA For Espionage For Leaking Secrets To The Press?

1.0 Introduction

This is a current affairs post, usually outside what I blog about.

I have found the count in the post title echoed in several publications, for example:

"...Historically, the vast majority of leak-related investigations have turned up nothing conclusive, and several of the nine that have been prosecuted — six already under the Obama administration, and just three more under all previous presidents — collapsed...

...Many people are surprised to learn that there is no law against disclosing classified information, in and of itself. The classification system was established for the executive branch by presidential order, not by statute, to control access to information and how it must be handled. While officials who break those rules may be admonished or fired, the system covers far more information than it is a crime to leak.

Instead, leak prosecutions rely on a 1917 espionage statute whose principal provision makes it a crime to disclose, to persons not authorized to receive it, national defense information with knowledge that its dissemination could harm the United States or help a foreign power." -- Charlie Savage, New York Times, 9 June 2012.

"Only three times in its first 92 years was the Espionage Act of 1917 used to prosecute government officials for leaking secret information to the press. However, the current administration has already brought six charges under this Act. The accused in all of these cases appear to represent whistleblowers, not those engaged in attempted espionage for foreign governments that 'aid the enemy.'" -- Association for Education in Journalism and Mass Communication

2.0 Possible List

Maybe these are those being discussed:

1. Daniel Ellsberg: Famous for the Pentagon Papers.
2. Anthony Russo: Also involved in disseminating the Pentagon Papers.
3. Samuel Loring Morison: Only person ever convicted, in a trial, for espionage for leaking classified information to the press.
4. John Kiriakou
5. William Binney.
6. J. Kirk Wiebe.
7. Ed Loomis.
8. Thomas Drake.
9. Bradley Manning: Involved with Wikileaks.

Apparently, Scooter Libby was not indicted and tried for espionage. The Espionage Act of 1917 was modified by the McCarran Internal Security Act of 1950, I guess.

3.0 Possible Future Additions

Possibly, Edward Snowden and Retired General James Cartwright (for leaking, maybe, about Stuxnet) will be added sometime to the above list.

(Somewhere in Democracy in America, as I remember it, Alexis de Tocqueville observes that political disputes in the United States almost always become legal disputes.)

Observations on the Great Gatsby Curve

In recent years, some economists have drawn attention to a correlation that has been dubbed the Great Gatsby curve.  In particular, countries that have more inequality in income also have less economic mobility.  (By the way, the curve seems misnamed: Jay Gatsby lived in a time a great inequality and managed to move from being very poor to being very rich.  But never mind that.)

My own view is that this correlation is not particularly surprising.  Let me give you an analogy to explain why.

Suppose we collected data on various chess clubs (nations).  In every club, we have data on each member's win-loss record over the year (income).  We can then measure the variance of individuals' win-loss records (inequality).  We can also measure how a person's win-loss record in one year predicts his win-loss record in the subsequent year (mobility).

Some clubs have a bunch of players with similar levels of skill at chess.  In this case, everyone would have a win-lose record that is close to each other, and a person's club ranking one year would not have a lot of predictive value for his ranking the next.  That is, we would have small inequality and substantial mobility.

Other clubs are more heterogeneous.  They have some masters and some novices.  The masters have much better records than the novices, and their better records tend to persist year to year.  That is, we would have substantial inequality and little mobility.

If we put all these clubs together in a scatterplot, we would get something close to the Great Gatsby curve.

Notice a corollary: Suppose we combined two clubs, one that with mostly masters and one with mostly novices.  The new combined club would be more heterogeneous and, therefore, would exhibit more inequality and less mobility than either of the clubs separately.

The application of this corollary to the Great Gatsby curve is that if we looked at Europe as a whole, rather than each nation separately, we would find that Europe as a whole has more inequality and less mobility than the individual countries.  That is, Germans are richer on average than Greeks, and that difference in income tends to persist from generation to generation.  When people look at the Great Gatsby curve, they omit this fact, because the nation is the unit of analysis.  But it is not obvious that the political divisions that divide people are the right ones for economic analysis.  We combine the persistently rich Connecticut with the persistently poor Mississippi, so why not combine Germany with Greece?

The bottom line for me that the Great Gatsby curve is a bit interesting, but neither particularly surprising nor suggestive of any specific conclusions or policy recommendations.

Krugman Deconstructed

Paul Krugman seems worried that Noah Smith has been bitten by a zombie, or otherwise thrown into a discombobulated state. Noah's sin is to have suggested that what is going on in a New Keynesian model may not shed much light on what is going on in Japan. The basic Woodford framework confines attention to sticky prices as a friction that creates inefficiency that can be corrected by monetary policy. Monopolistically competitive firms can change prices infrequently - say, through a Calvo pricing mechanism - and unanticipated shocks can lead to relative price distortions that monetary policy can act to mitigate. But, those relative price distortions will disappear in the long run as prices adjust. Noah seems to think that 20 years (in the Japanese case) gets us pretty close to full adjustment, and I agree. Indeed, with the frequency of price changes we observe in the data (e.g. Klenow et al.), the same argument would seem to apply to our current predicament. It has been five years since the shock hit that produced the last recession in the United States. If we think that the current state of the US economy is somehow inefficient - i.e. there is some set of policies that could improve matters - it seems we should not be thinking about sticky prices as the source of that inefficiency.

But in another sense, Noah is incorrect:

This New Keynesian model corresponds nicely to the simple AD-AS model that people learn in Econ 102.

You can forgive Noah for thinking this, as a lot of effort on the part of Woodford (in his book and published papers) and other New Keynesians has has gone into making it appear that New Keynesian economics is somehow the same thing as AD-AS, or in fact an excuse for taking that shortcut. The basic New Keynesian model is actually a real business cycle model with Dixit-Stiglitz monopolistic competitors and sticky prices, which owes more to Ed Prescott than to Keynes. Without the word "Keynesian" attached to it, Keynes would not recognize the structure as having anything to do with him, and it's doubtful the first person who put an AD-AS model into an undergraduate textbook would recognize it either.

Krugman is certainly sold on the idea that AD-AS and Woodford macroeconomics are the same thing. According to Krugman, we can do really well with AD-AS, though sometimes we might have to "check" what we are doing by going to the full-blown New Keynesian model. In the case of Noah's post, Krugman thinks Noah's analysis is flawed because of his failure to take account of the liquidity trap, and otherwise falling short in adhering to Krugman's talking points.

Krugman has two models he likes to think about. One is AD-AS, and the other is in his paper with Eggertsson. But he wants to think of those as the same thing. So let's take the AD-AS route, as that's easier. What is Krugman trying to say? Set the wayback machine, Sherman, and off we go. I'm now imagining myself in a macro class in 1975, where I learned what was in the first edition of Branson's book. This is something like playing with an 8-track player you found in your basement. The thing works - in the sense that you can make it do what it was built to do - but you know while playing with it that you are wasting your time.

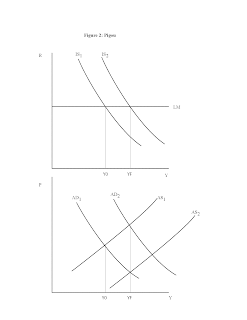
Figure 1 shows you the IS-LM, AD-AS part of the model. This is the liquidity trap case. The LM curve is flat. Equilibrium output Y0 is less than full employment output YF. Why is the AD curve vertical? That's because changes in prices don't do anything in the IS-LM portion of the diagram, as real money demand is perfectly elastic at the zero lower bound. So, in the absence of some kind of intervention, this economy remains stuck below full employment forever. The fix is fiscal policy - increase G, shift the IS curve, and we go to full employment output.

But, as I was taught in my intermediate macro class, Pigou had a fix for this. If there's a wealth effect on consumption, for example, then you get a downward-sloping AD curve, as in Figure 2. In the short run, output is less than full employment, but if we let prices adjust, then over time the nominal wage falls, shifting AS to the right, and we get full employment. But the short run fix, as in Figure 1, is fiscal policy, which gets us there faster without the bother of waiting for the price adjustment.

But Figures 1 and 2 are not what Krugman has in mind. He's barking up Kalecki's tree, apparently. Kalecki argued that a deflation would increase the real value of debts denominated in nominal terms, and that the wealth effect would go the other way. This gives you a positively-sloped AD curve, which Eggertsson and Krugman indeed coax out of their New Keynesian model.

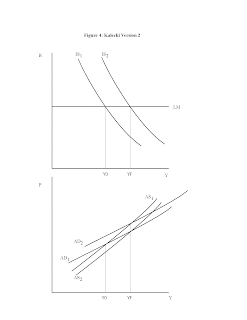
The key question is, with the Kalecki effect in there, is the slope of the AD curve greater or less than the AS curve? Let's do it both ways. First in Figure 3, suppose AD is steeper than AS. In this case, long-run adjustment to full employment occurs through an increase in the nominal wage. This occurs because there is an excess demand for labor. But I don't remember Krugman arguing that the labor market is currently too tight (maybe you do?). He must be thinking about the other case.

So, in Figure 4, AS is steeper than AD. In this case, in the long run we have to wait for the nominal wage to fall, shifting AS to the right. Krugman says that wages are really sticky downward, so we don't want to wait that long. What's the short-run cure? Well, the problem is that there is too much aggregate demand. We want to shift AD to the left. Austerity will work nicely. Again, I don't remember Krugman pushing for that, but maybe you do.

Krugman might want to appeal to Eggertsson/Krugman as the ultimate truth with respect to issues he discusses in his blog, but that paper has its own problems. It's a superficial treatment of debt contracts and default, and uses linearization to characterize the zero-lower-bound equilibrium, which is known to be misleading.

These are the basics of Krugman's narrative:

1. Most of the macroeconomics done since 1970 was a waste of time.
2. The exception to (1) is New Keynesian economics.
3. New Keynesian economics and textbook AD-AS are essentially the same thing.
4. Wages and prices are sticky.
5. Wage and price stickiness are the primary source of current inefficiencies in the U.S. economy.
6. Relative to what is efficient, GDP is currently too low, and the unemployment rate is too high.
7. We can correct the inefficiencies that currently exist with an expansion in government expenditure on goods and services.

That narrative is a web of contradictions, and hardly internally consistent science. The AD-AS model somehow persists in textbooks, which causes it to retain its power as a tool for communicating with people who have only a smattering of economics training. Krugman exploits that, and so have New Keynesians, but that behavior doesn't serve the cause of science.

Who will the next Fed chair be?

Janet Yellen is the odds-on favorite.

Rate of Profits And Value Of Stock Independent Of Workers Saving

.

1.0 Introduction

This post presents elements of a model of a smoothly reproducing economy, that is, of an economy growing along at the warranted growth rate. I have previously presented a more detailed exposition of a variant of this model. One could add, say, Harrod-neutral technical change to that exposition. I would find it easier to add biased technical change by assuming fixed, not variable, coefficients of production. Perhaps this model reflects conventions and the balance of class forces prevalent in Anglo-American economies after World War II and before the collapse of the Bretton Woods system.

Anyways, I am revisiting this model because, recently, I have noticed another mathematical property of this model. Not only are the determinants of the rate of profits along a warranted growth path independent of the decisions of the workers to save. So is the average stock price of corporations.

2.0 The Model

This model abstracts from the existence of government spending and taxation. It also treats foreign trade as negligible. National income is comprised of wages, W, and profits, P. The rate of profits, r, is the ratio of profits to the value of capital goods, K, used in producing national income.

2.1 The Corporate Sector

I begin with corporations. The corporations own the capital goods and hire the workers to produce output with these capital goods. Corporate managers decided on the level of investment, I, to achieve a target growth rate, g.

Investment, in this model, is financed by some mixture of retained profits and the issuance of new stock (also known as shares) on the stock market. Corporate managers decide on this mix. Let s_c be the proportion of profits that are retained to finance new investment. And let f be the proportion of investment financed by issuing new shares:

I = s_c P + f I

Some algebra yields:

P/K = [(1 - f)/s_c] (I/K)

Or:

r = [(1 - f)/s_c] g

Thus, the rate of profits consistent with a warranted rate of growth is determined by parameters characterizing decisions made by corporate managers.

2.2 Finances and Households

In this model, households do not own capital goods. Rather, corporations own capital goods, and households own stock in these corporations. The ratio of the market value of stock to the value of the capital goods owned by the corporations is called the valuation ratio, v. The valuation ratio is assumed constant along a warranted growth path. Variations in the valuation ratio reflect short-term speculation. Generally, the valuation ratio is above unity.

Households are divided into two classes in this model, workers and capitalists. Workers receive part of their income in the form of wages. Given a positive savings rate on the part of workers, they also receive dividends and capital gains from their stock. Capitalists do not labor; their households receive all their income from dividends and capital gains. The variable j is used to denote the proportion of stocks owned by the workers.

Dividends consist of profits received and not retained by the corporations. By assumption, the value of dividends is then (1 - s_c)P. Net investment, I, is the increase in the value over a year of the capital goods owned by corporations, while the increase in the value of stocks is vI. But the value of new shares is only fI. The difference, (v - f)I, is the value of capital gains.

The interest rate is the ratio of the returns to financial capital (that is, dividends and capital gains) to the value of stock. With a valuation ratio above unity the interest rate, i, falls below the rate of profits. The valuation ratio then becomes:

v = (r - g)/(i - g)

I assume workers typically save at the rate s_w, and capitalists typically save at the greater rate s_r. Table 1 shows sources of savings, based on these definitions and behavioral assumptions.

Table 1: Sources of Economy-Wide Savings

Source	Amount
Retained Earnings:	sc P
Capitalist Savings Out of Dividends:	(1 - j)sr(1 - sc)P
Minus Capitalist Consumption Out of Capital Gains:	- (1 - j)(1 - sr)(v - f)I
Worker Savings Out of Wages:	swW
Worker Savings Out of Dividends	j sw(1 - sc)P
Minus Worker Consumption Out of Capital Gains:	- j(1 - sw)(v - f)I

In adding up savings, one must be sure not to double-count retained earnings. Corporations decide to save retained earnings, but households can undo this decision by consuming capital gains. Total savings for capitalists, S_r, are:

S_r = (1 - j) s_r[(1 - s_c)P + (v - f)I]

Total savings for workers, S_w, are:

S_w = s_wW + j s_w[(1 - s_c)P + (v - f)I]

Along a warranted growth path, investment is always equal to savings. The following equation is based on the components in Table 1:

I = s_c P + (1 - j)[s_r(1 - s_c)P - (1 - s_r)(v - f)I]

+ s_wW + j [s_w(1 - s_c)P - (1 - s_w)(v - f)I]

A bit of algebra allows the investment-savings equality to be restated:

I = s_c P + S_r + S_w - (v - f)I

The last term (that is, capital gains) is subtracted to avoid double-counting.

Another condition of a warranted growth path in this model is that the corporate sector, capitalist households, and workers continue to endure. This condition requires that the rate of growth of the book-value of the capital goods held by the corporations, the rate of growth of the value of the stock held by capitalists, and the rate of growth of the value of the stock held by the workers all be equal. Thus, the rate of growth of the value of the stock held by capitalists is:

g = S_r/[(1 - j)v K]

The rate of growth of the value of the stock held by workers is:

g = S_w/(j v K)

This completes the exposition of the equations I need for my point here.

2.3 Some Algebra

I now report on some algebraic manipulations of these equations. The condition that the value of the stock held by capitalists and workers grows at the same rate yields the following condition:

S_w = S_r [j/(1 - j)]

Substituting in the investment-savings equality, one can obtain:

I = s_c P + [S_r/(1 - j)] - (v - f)I

Or, by expanding the definition of capitalist savings:

I = s_c P + s_r[(1 - s_c)P + (v - f)I] - (v - f)I

Regrouping yields:

[1 + (1 - s_r)(v - f)]I = [s_c + s_r(1 - s_c)]P

Dividing through by the book value of the capital goods owned by the corporations, one obtains:

r = {[1 + (1 - s_r)(v - f)]/[s_c + s_r(1 - s_c)]} g

Equating for the value of the rate of profits previously found, one obtains an expression for the valuation ratio in terms of model parameters:

v = {[s_r(1 - s_c)]/[s_c(1 - s_r)]} - {s_r/[s_c(1 - s_r)]} f

Notice the parameters on the right-hand-side characterize either corporate decisions or the decisions of capitalist households. The saving propensities of the workers do not enter into it. The more that corporations finance investment by issuing shares, instead of using retained earnings, the lower the valuation ratio is along a warranted growth path. If the proportion of profits distributed in dividends lies below the proportion of investment financed by issuing new stock, a smaller capitalist savings propensity is associated with a higher valuation ratio. In some sense, capitalists get what they spend.

3.0 Conclusions

This post has outlined some necessary properties of a warranted growth path in a model containing:

• Corporations, a capitalist class, and a class of workers.
• A stock market, in which ownership shares in the corporations are bought and sold.
• A growth rate determined by decisions of the corporate managers.

In this model, the decisions of the corporate manager as to the growth rate, retained earnings, and finance obtained by issues of new stock determine the rate of profits consistent with a warranted growth path. These decisions of the corporate managers, along with the savings propensities of the capitalists, determine the ratio of the price of stock to the book value of the capital goods owned by the corporations. A fortiori, these decisions also determine the interest rate. Within the limits where a warranted growth path exists, the savings propensities of the workers have no effect on the growth rate, the rate of profits, the price of stock, the interest rate, or the functional distribution of income. The savings decisions of the workers do affect, however, the personal distribution of income and the proportion of stock owned by the workers.

Appendix: Variable Definitions

• K is the book value of the capital goods, in numeraire units, owned by the corporations.
• I is investment, in numeraire units.
• P is corporate profits, in numeraire units.
• S_r is capitalist savings, in numeraire units.
• S_w is worker savings, in numeraire units.
• f is the proportion of investment financed by issuing new stock (also known as shares).
• g is the warranted rate of growth.
• i is the interest rate.
• j is the proportion of stock owned by workers.
• r is the rate of profits earned by the corporations on the book value of their capital stock.
• s_c is the proportion of profits retained by corporations.
• s_r is the (average and marginal) to save of the capitalists.
• s_w is the (average and marginal) to save of the workers.
• v is the valuation ratio, that is, the ratio of the value of the stocks of the corporations to their book value.

Reference

• Scott J. Moss (Dec. 1978). The Post-Keynesian Theory of Income Distribution in the Corporate Economy, Australian Economic Papers, V. 17, N. 31: pp. 302-322.

Selgin on Gorton

I ran across an interesting piece by George Selgin. He makes a point that a lot of people miss, including, in this case, Gary Gorton. History gives us useful information for organizing our thinking about financial crises (and other events of course), but many people attach too much weight to U.S. experience. This matters in particular for how we address the issue of whether financial fragility is inherent or induced.

If we confine our attention to U.S. financial history, we might think that banks are inherently unstable, as Diamond and Dybvig theorized. We also might think, if we look at the performance of behemoths like Bank of America and Citigroup, that too-big-to-fail could be an inherent problem in banking. But, as Selgin points out, the notion that banking arrangements are inherently prone to panics and too-big-to-fail problems flies in the face of experience in other countries - Canada in particular.

The kind of thinking Selgin objects to leads to inappopriate policy conclusions. Gorton in particular seems to subscribe to the idea that a fix which will make the banking system safe is some version of narrow banking - restricting what financial intermediaries can hold as assets to back any type of transactions account. But there are other - and seemingly better - ways to get safety (if you want it), as the Canadians have shown.

Against Biotechnological Determinism

1.0 Introduction

Perhaps arguments lasting between groups for decades have some underlying issues that are not immediately apparent by looking at the details. I often attempt to explain technical details of the Cambridge Capital Controversy (CCC). Is there something central, but hardly articulated by the participants and on-lookers, that helps in understanding the positions taken by economists on the CCC? I take the concept and the phrase biotechnological determinism from Stephen Marglin (1984).

2.0 Neoclassical Economics As Embodying Biotechnological Determinism

A naive neoclassical economics embodies biotechnological determinism. The biology is to be seen in population demographics and in preferences, including over intertemporal consumption plans and over choices between labor and leisure. The technology is to be seen in production functions and endowments.

From about 1870 up to the 1930, neoclassical economists emphasized incoherent models of long-run equilibrium. To maintain biotechnological determinism after the transition to very short-run models of temporary and intertemporal equilibrium, neoclassical economists must adopt a theory of the short-run. The most congenial short run models to this determinism will assume all markets always clear.

3.0 Post Keynesianism Rejects Biotechnological Determinism

Post Keynesians, as I see it, reject biotechnological determinism. Here are some characteristic ideas of Post Keynesianism that, at least, are in tension with such determinism:

• An emphasis on open models.
• A view that appropriate models might vary among countries, sectors, and decades.
• An emphasis on historical time and the acceptance or development of models in which history matters.
• The adoption of models in which corporations are taken as having power to make decisions on the rate of growth and the markup of prices over costs.
• The rejection of the descriptive accuracy of the autonomous utility-maximizing consumers.
• The rejection of the natural rate of unemployment.
• The rejection of the Wicksellian concept of the natural rate of interest, in all runs.
• The acceptance of the idea that fiscal policy can be effective.

4.0 Can Mainstream Economists Reject Biological Determinism?

Of course, markets do not always clear in neoclassical economics. For decades, economists have been talking about, for example, sticky prices, asymmetric information, and multiple equilibrium. Nevertheless, I am often surprised by how willing many economists who have studied such matters seem to be willing to talk as if the economy is always trending towards a unique, given long-run equilibrium. Forces that prevent the economy reaching equilibrium in the short run seem to have no effect on the long run theory. Maybe a tension exists in neoclassical economics between the formal properties of the theories that have been developed and the underlying vision of many economists.

Some argue that mainstream economics is no longer neoclassical and, at least at the research level is open to a wide variety of ideas. Some recent ideas, such as evolutionary game theory, seem compatible with outcomes emerging that cannot be calculated in a closed-form solution as uniquely determined by the givens of the model.

I think older trends, emphasizing perfect competition and instantaneous adjustment to equilibrium, are still widely prevalent among economists and how economists portray their ideas to the public. A skeptic might argue that newer trends will never replace such ideas because of their incompatibility with this underlying vision of biotechnological determinism.

5.0 Conclusion

Do different views on biotechnological determinism underlie the visions of various economists? Can contrasting views on this issue ever be settled by empirical evidence, and if so, how?

Bibliography

• Stephen A. Marglin (1984). Growth, Distribution, and Prices, Harvard University Press.

The Fed's First 100 Years

I spent today at the NBER's conference celebrating the 100th anniversary of the Federal Reserve. Among the conferences I have attended over the years, this was among the best. You can find the papers presented here.

Who should the next Fed chair be?

A friend points out to me that the monkeys over at Economics Job Market Rumors are voting whether they would prefer Janet Yellen or Larry Summers as the next Fed chair.  Right now, it is close to a tie.

Summers on the Corporate Tax

On the issue of corporate tax reform, Larry Summers tries to forge a compromise:

The United States should eliminate the distinction between repatriated and unrepatriated foreign corporate profits for U.S. companies and tax all foreign income (after allowances for taxes paid to other governments) at a fixed rate well below its current corporate rate, perhaps in the range of 15 percent.

Sraffa Prices As A Linear System

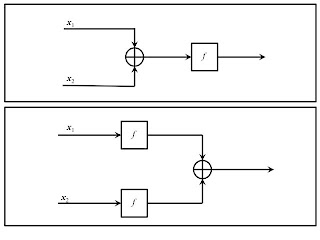Figure 1: Two Equivalent Block Diagrams for a Linear System

1.0 Introduction

I have previously gone on about complex, out-of-equilibrium phenomena arising in certain non-linear models for economics. This post provides a contrast, by defining linear. Sraffa's system of equations for prices of production, from a certain perspective¹, is an example of a linear system.

I regard the mathematical manipulations expressed in this post as fairly trivial. Nevertheless, it will not surprise me if some find it difficult to read. I do not think any such reading difficulties result solely from defects in my expository powers. Rather, I am trying to echo the sort of abstract reasoning typical of advanced mathematics courses taught at many universities. I think I only gesture here at the advantages provided by such abstractions.

2.0 Definition of "Linear"

Functions can be characterized as linear or non-linear. A function, f(), maps elements in some set to elements in another, possibly different, set. The set of possible arguments² for a function is known as the domain of the function. The set that elements of the domain are mapped into is known as the range of the function. One assumes that elements of the domain can be added together, in some sense, to obtain another element of the same set. Furthermore, each element of the domain can be multiplied by a scalar³. Last, one makes the same assumptions about the elements of the range.

The function f is linear if the following two conditions are met:

f(x₁ + x₂) = f(x₁) + f(x₂)

f(a x) = a f(x)

These equations are illustrated, respectively, by Figure 1 above and Figure 2 below. The first condition states that when a linear function is applied to the sum of two elements, the summation can equally well be calculated after applying the function to the elements being summed. The second condition states that the order of scalar multiplication and the application of the function can likewise be interchanged, with no effect on the output.

Figure 2: Two More Equivalent Block Diagrams for a Linear System

Maybe the simplest example of a linear system is the equation of a straight line going through the origin:

y = f(x) = m x,

where x and y are real numbers⁴.

3.0 Sraffa's Price Equations

The above definition would not be worth much if the only example of a linear function was a straight line through the origin in a two-dimensional Cartesian space. Accordingly, I will describe an example for a function whose argument is a vector.

Suppose an economy is observed at a point in time. And, in this economy, at the observed scale, firms have adopted n processes to produce n commodities. The j-th process is characterized by its inputs and outputs. Its inputs consist of a_0,j person-years of labor, a_1,j units of the first commodity, a_2,j units of the second commodity, and so on. Its outputs consist of b_1,j units of the first commodity, b_2,j units of the second commodity, and so on⁵. A common rate of profits, r, is also among the givens in this model. These givens allow one to set up the following system of equations for the wage, w, and prices of production⁶, p₁, p₂, ..., p_n:

(p₁ a_1,1 + ... + p_n a_n,1)(1 + r) + a_0,1 w = p₁ b_1,1 + ... + p_n b_n,1

(p₁ a_1,2 + ... + p_n a_n,2)(1 + r) + a_0,2 w = p₁ b_1,2 + ... + p_n b_n,2

.
.
.

(p₁ a_1,n + ... + p_n a_n,n)(1 + r) + a_0,n w = p₁ b_1,n + ... + p_n b_n,n

The above system of n equations in n + 1 unknowns can be conveniently expressed in matrix form:

p A(1 + r) + a₀w = p B,

where a₀ and p are row vectors and A and B are square vectors. Some manipulations yields the following matrix equation:

p [B - A(1 + r)] - a₀w = 0

These manipulations suggest the definition of a linear function.

3.1 A Linear Function

Accordingly, consider the following function:

f(p, w) = p [B - A(1 + r)] - a₀w

This function maps a vector space with the dimension n + 1 to an n-dimensional vector space. Figure 3 illustrates for the case where n is two. The components of the vector calculated by this function are the extra profits earned in each process in use. Two, almost one-line, proofs demonstrate the linearity of this function.

Figure 3: A Linear Function for a Two-Commodity Economy

3.1.1. Proof of the First Condition

By definition, the value of the function for the sum of two elements of its domain is:

f(p + q, u + v) = (p + q) [B - A(1 + r)] - a₀(u + v)

Or:

f(p + q, u + v) = p [B - A(1 + r)] - a₀u + q [B - A(1 + r)] - a₀v

Or, by the definition of the function:

f(p + q, u + v) = f(p, u) + f(q, v),

which was to be shown.

3.1.2. Proof of the Second Condition

By definition, the value of the function for an argument consisting of the product of a scalar and an element of the domain of the function is:

f(c p, c w) = (c p) [B - A(1 + r)] - a₀(c w)

Or:

f(c p, c w) = c { p [B - A(1 + r)] - a₀w}

Or, by definition,

f(c p, c w) = c f(p, w)

which, again, was to be shown.

3.2 Observations and Questions

Consider all the elements of the domain of a function that map into the zero element in the range. This subspace of the domain is called the null space⁷. Figure 4 illustrates a null space for a linear function that, generically, does not arise for the Sraffa model. The three dimensions in the figure represent the domain of the function. For a linear model, the origin is in the null space. In this case, two non-zero independent vectors, represented by the two heavy arrows not along any of the three axes, map to zero. So the plane in which these two vectors lie represents the subset of the domain which maps to zero.

Figure 4: The Subspace of Zeros of a Linear Function

Wages and prices of commodities are positive in an economically meaningful solution to Sraffa's model. Thus, the null space should contain a ray leading from the origin through the first quadrant. Furthermore, if the extension of such a ray is all of the null space, the solution of this model is unique, up to multiplication by a constant. Choosing a numeraire for measuring prices and the wage specifies a location on this ray.

The economic setting of this model suggests conditions⁸ that might lead to the desired properties of the null space:

• No coefficients of production are negative, while direct labor inputs are always positive.
• Every process requires some commodities as inputs, and produces at least some commodities.
• Every commodity is produced as an output by at least some process.
• The economy hangs together, in some sense. One cannot find two or more sets of commodities where, for instance, no commodities from the first set enter as inputs into the second set and vice versa.
• The production processes are all distinct, in some sense. Technically, no production process is a linear combination of the other processes.
• The economy produces a surplus. The quantities of commodities required as inputs can be replaced out of the outputs, with some commodity output left over.
• With a notional rescaling of processes, a set of commodities can be found that, in some sense, enter into the production of all commodities and that are being produced at a same rate of surplus production.
• The rate of profits does not exceed that maximum rate of surplus production.

More is going on here than a counting of equations and variables.

4.0 Conclusion

Sraffa, in his book, does not present his sequence of models in these abstract terms. But many comments and sections, such as the appendix on "beans", demonstrate that he was aware of the mathematical issues arising with his models. One can read Sraffa as having an interest in computability not shown in my exposition.

Finally, this post proves that the use of models in which the solution illustrates the mutual interdependence of a system of equations is simply insufficient to demonstrate that economists think of the economy as a complex, non-linear system.

Footnotes

1. If one took the wage, instead of the rate of profits, as the independent variable, Sraffa's equations would define a non-linear system. Furthermore, since Sraffa's model is open, it is consistent with non-linearities in economic relationships not in the model, such as provided by Increasing Returns to Scale.
2. In this section, arbitrary elements of the domain are represented by x, x₁, and x₂.
3. Technically, the domain and the range are each examples of a vector space, also known as a linear space. The scalars are from a field. The sets of real and complex numbers are canonical examples of a field.
4. Although the graph of an affine function, y = m x + b, is a straight line, an affine function is, technically, non-linear when the y-intercept is non-zero.
5. Since more than one commodity can be produced as output for each process, this is a model of joint production. See Chapter VII, Sections 50-52 of Production of Commodities By Means of Commodities.
6. Prices of production allow for the outputs to be redistributed among industries such that the economy can continue (re)production undisturbed.
7. For a linear function, the null space is a linear space.
8. Such conditions are more obvious for the special case of no single-product industries. I do not fully understand the issues for joint production, especially when the processes in use are chosen from a larger set of possible processes.

Warren Mosler On Front Business Page Of New York Times

Anne Lowrey provides a profile of Warren Mosler and Modern Monetary Theory. I am sitting in my favorite coffee shop, when I open my newspaper to this article. I say, "Hey, I know this guy. I once sold him a book on-line." But I did not go on about economics. I know the fellow next to me is a fan of Formula 1 racing. So I say, "He has his own car company. He makes race cars, I think." And I skim forward to the third to last paragraph, skipping over quotes from professors at the University of Missouri at Kansas City and such like, to read about Mosler Automotive, which apparently he is looking to sell.

Cengage

Over on his blog, Paul Krugman calls attention to the Cengage bankruptcy.  I am not sure why he thinks this event is noteworthy.  He seems to do so because Cengage is the publisher of my favorite textbook. I suppose it is schadenfreude on Paul's part.

If you are interested in the topic, I suggest you read this article.  The short story is that this is a Chapter 11 bankruptcy (a reorganization), not a Chapter 7 bankruptcy (a liquidation).  These are very different things. In this case, the equity holders are being wiped out, and the debt holders are the new equity holders.  Otherwise, not much is happening.  As the article states:

The transaction is expected to be largely a non-event for others doing business with Cengage. The company has permission from the lenders to keep using cash flow from operations to fund the business, and expects to keep paying vendors, authors’ royalties, and employees on schedule. (Since Cengage has substantial cash balances—a vendor Frequently Asked Questions document estimates the company’s liquidity at approximately $280 million—and expects to generate positive cash flow, it does not need debtor-in-possession financing.) The company plans to keep delivering orders in full, is not planning to renegotiate any customer contracts except as they expire as usual, and is continuing to launch new products.

So if you are a user of my favorite textbook, rest assured that it is business as usual.

Elsewhere

• Frances Woolley claims that, nowadays, economics is more empirically grounded and better than it used to be.
• Edward Fullbrook says that academic success in economics is furthered by publishing papers that serve best as manure and hindered by publishing serious work.
• Noah Smith describes what he calls four levels of science.

(It would be nice to have a catalog of responses to Greg Mankiw's latest vicious tomfoolery, to be published in the Journal of Economic Perspectives.)